[백준/누적합] 3020 개똥벌레

3020번: 개똥벌레

---

문제 이해하기

n = 14, h = 5

 

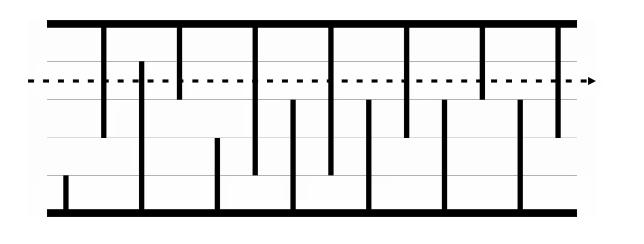
개똥벌레가 동굴을 지날 때 뚫어야하는 장애물의 최소 개수와 그 층 ?

 

 

예시와 같이 5개의 층이 있는 동굴에서 몇 층을 지나가야하는지 구해야한다.

각 층별로 장애물의 총 개수를 확인한다. 장애물 개수가 가장 작은 층들이 정답이 된다. 

 

각 층의 장애물 개수를 나타내는 리스트를 만들고, 장애물을 하나씩 조사하며 높이에 맞게 리스트 요소를 업데이트 해준다.

즉, 리스트 = 동굴, 리스트 인덱스 = 각층, 리스트 요소 = 장애물의 개수가 된다.

 

 

• lst = [0] * 5 (5개의 층)
• for문으로 장애물을 하나씩 순회
• 짝수번째 장애물은 0번 인덱스부터, 홀수번째 장애물은 마지막 인덱스부터 장애물의 길이만큼 +1 한다.
• 즉, 0번 장애물 → lst = [1, 0, 0, 0, 0], 1번 장애물 → lst = [1, 0, 1, 1, 1]

 

 

그런데 이 풀이로는 시간초과가 난다. 각 장애물 길이만큼 for문이 또 도는 것이 문제인 것 같다.

 

따라서 누적합 개념을 적용하여 장애물 길이만큼 전부 1씩 더해주는것이 아니라, 장애물의 처음과 끝만 기록하고 누적합을 사용하여 각 층별 장애물의 개수를 계산한다.

---

풀이

# 1. 입력받기
n, h = map(int, input().split(" "))

# 2. 각 장애물의 시작과 끝만 기록
lst = [0] * h

for i in range(n):
    stick = int(input())

    # 짝수면 0에서 시작
    if i % 2 == 0:
        lst[0] += 1
        lst[stick] -= 1

    # 홀수면 h-1-stick 에서 시작
    else:
        lst[h-stick] += 1

# 3. 누적합으로 각 층별 장애물 개수 계산
for j in range(1, h):
    lst[j] += lst[j-1]

# 4. 최소값과 그 층의 개수
minV = min(lst)
cnt = 0
for n in lst:
    if n == minV:
        cnt += 1

# 5. 정답 출력
print(minV, cnt)

---

풀이과정

장애물이 시작하는 층에 +1

누적합을 사용하므로 장애물의 시작점에만 1을 더 해주면 그 윗층부터는 1을 해당 층에 직접 더해주지 않아도 그 전 층에 있던 장애물의 개수까지 고려한다. 

 

장애물이 끝난 직후의 층에 -1

첫 번째 장애물의 경우 0번 층까지만 존재한다.

그런데 누적합을 사용하면 1번 층의 장애물 개수에 0번 층의 장애물 개수까지 더해진다.

따라서 1번 이상의 층에는 해당 장애물이 반영되지 않도록 -1을 해준다.

 

위에서 내려오는 장애물

항상 가장 윗층까지 연결되어 있으므로 끝나는 지점을 표시할 필요가 없다.

따라서 시작하는 층에 +1만 해준다.